how to find speed of a wave

The wave equation and wave speed.

This is a support page to the multimedia chapter Travelling Waves II in the volume Waves and Sound. It gives background information and further details. Deriving the wave equation A solution to the wave equation Speed of a wave in a stretched string The wave speed depends on tension We shall give qualitative physical explanations as well as the mathematics. However, before starting this section, you may wish to revise calculus.

---

In the chapter Travelling waves I, we described the travelling wave and some of its properties. It's time to analyse it, again using the stretched string as a simple case on which to start. As is usual in analysing motion, we start with Newton's second law of motion. The acceleration is a differential of position with respect to time, so this will give us a differential equation. The total force acting on a segment of a stretched string depends on the shape of the string, which depends on the differential of displacement with respect to position along the string. This gives us the speed of the wave. More simple mechanics gives the expression for power transmission. Finally we define intensity and briefly look at radiation in two and three dimensions.

Deriving the wave equation

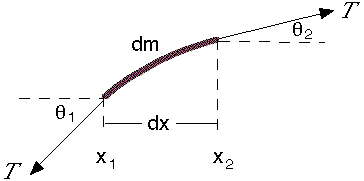Let�s consider a string that has mass per unit length is μ. It is stretched by a tension T, which is much larger than the weight of the string and its equilibrium position is along the x axis. This diagram shows a short section of the string, stretched in the x direction, and the forces acting on it. Our analysis only applies for small deformations, for which the string is a linear medium, and we neglect the gravitational force on the string (which in any case is constant).

One consequence of this restriction to small deformations is that the angle θ between the string and the x direction is much smaller than 1, so sin θ  ≅  θ and cos θ  ≅ 1. (On our diagram, however, the deformation has been exaggerated for clarity.) It also follows that the length of the segment shown is dx.

Let's apply Newton's second law in the vertical y direction:

F_y  =  ma_y.

The sum of forces in the y direction is

F_y  =T sin θ₂ −T sin θ₁.

Using the small angle approximation, sin θ ≅ tan θ = ∂y/∂x. So we may write:

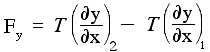
So the total force depends on the difference in slope between the two ends: if the string were straight, no matter what its slope, the two forces would add up to zero. Now let's get quantitative. The mass per unit length is μ, so its mass dm = μdx. The acceleration in the y direction is the rate of change in the y velocity, so a_y  =  ∂v_y/∂t  =  ∂y²/∂t². So we can write Newton�s second law in the y direction as

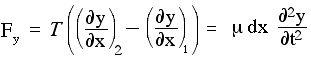
Rearranging this gives

Now we have been using the subscript 1 to identify the position x, and 2 to identify the position (x+dx). So the numerator in the last term on the right is difference between the (first) derivatives at these two points. When we divide it by dx, we get the rate of change of the first derivative with respect to x, which is, by definition, the second derivative, so we have derived the wave equation:
So the acceleration (on the left) is proportional to the tension T and inversely proportional to the mass per unit length μ. It is also proportional to ∂y²/∂x². So the a greater curvature in the string produces a greater acceleration and, as we have seen, a straight portion is not accelerated. The confirms what we have seen qualitatively in Travelling waves 1. This is the wave equation in one dimension. Now it is time to solve it.

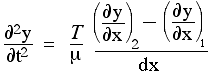
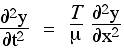
A solution to the wave equation

The wave equation is a partial differential equation. We discuss some of the tactics for solving such equations on the site Differential Equations. One of the most popular techniques, however, is this: choose a likely function, test to see if it is a solution and, if necessary, modify it. So, let's use what we already know. We know that sine waves can propagate in a one dimensional medium like a string. And we know that any function f(x − vt) is a wave travelling at speed v. In the first chapter on travelling waves, we saw that an elegant version of the general expression for a sine wave travelling in the positive x direction is y  =  A sin (kx − ωt + φ). A suitable choice of x or t axis allows us to set φ to zero, so let's look at the equation
y  =  A sin (kx − ωt)

to see whether and when this is a solution to the wave equation

In taking the partial derivative with respect to t, we hold x constant and vice versa. So, remembering that the derivative of sine is cos and that the derivative of cos is minus sine, we can write the first two partial derivatives with respect to t and x like this:
which we can also see below, as functions of x by graph and as functions of t by animation.

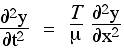
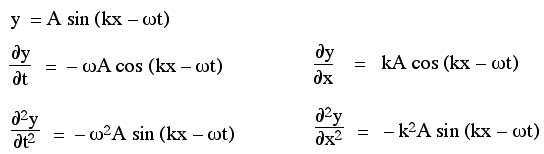
Wave speed in a stretched string

So we have seen that the second partial derivatives have the correct shape, which means we are on the right track. However, to be a solution to

the partial derivatives
must not only have the correct shape, but also the correct ratio. In other words, y  =  A sin (kx − ωt) is a solution, provided that

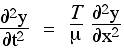
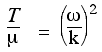
In Travelling waves II, we saw that the ω/k was the wave speed v, so we now have an expression for the speed of a wave in a stretched string:

Happily, we see that the wave speed is greater for a string with high tension T and smaller for one with greater mass per unit length, μ. While we are here, we should note that this specific example of the wave equation demonstrates some general features. Usually, it is possible to think of the speed of a wave like this
A digression. We discuss the speed of sound later, but note here that, for sound, the inertial property is the three dimensional density, ρ, rather than the one dimensional density μ. The restoring property for sound is the adiabatic bulk modulus of the air, γP_A. γP_A is like a three dimensional 'spring constant', where P_A is the atmospheric pressure and γ is a numerical constant associated with adiabatic (rapid) deformations. So the speed of sound is v  =  √(γP_A/ρ).

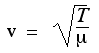
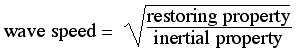
For the speed of electromagnetic waves, one can think of the electric effects as being restoring (the field created by separating positive and negative charges tends to reunite those charges) and the magnetic effects as being, in a general sense, 'inertial', insofar as a magnetic field, once created, tends to maintain itself (the Faraday field opposes changing the magnetic flux). So, in terms of the Coulomb constant k_C and Coulomb's constant for magnetism, k_m, we can write c  =  √(k_C/k_m), which we more usually write as c  =  1/√(ε₀μ₀). See the section on Maxwell's equations.

The wave speed depends on tension

The two clips show the same rope, stretched over the same distance. As the stills show, the tension in the two cases differ by a ratio of approximately 4: in the first, the rope is stretched by the weight of two one-kg masses, in the second eight masses are used. So, with the same value of μ (the rope is negligibly stretched by these tensions), we should expect a ratio of speeds of √(8/2) = 2.

To transmit a wave pulse, power is being transmitted down the string.  In the next support page, we look in detail at wave power, intensity and radiation.

how to find speed of a wave

Source: https://www.animations.physics.unsw.edu.au/jw/wave_equation_speed.htm

Posted by: sauermazint.blogspot.com

Share this post